| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- php 프로그래밍 입문
- php 프로그래밍 입문 예제
- php 프로그래밍
- 백준
- Flutter
- 배열
- 최단 경로
- 페이코 추천인코드
- 한정 분기
- 플러터
- C언어
- 페이코 초대코드
- SWEA
- 플러터 개발환경 설정
- php 프로그래밍 입문 3판
- JAVA SPRING
- php 프로그래밍 입문 문제풀이
- C
- 자바 스프링
- 스프링
- 페이코 추천인
- php 프로그래밍 입문 연습문제
- programmers
- 파이썬
- php 프로그래밍 입문 솔루션
- 페이코 친구코드
- spring
- Java
- 자바
- php
- Today
- Total
ImJay
0-1 Knapsack Problem - 최고 우선 검색을 사용한 한정분기 (Branch and Bound) 본문
0-1 Knapsack Problem
최고 우선 검색을 사용한 한정분기 (Branch and Bound)
서론
한정 분기 전략의 동기 : 되추적의 비효율되추적의 탐색 과정에서 Valid가 적용되더라도 여전히 상당한 비율의 정점을 방문하지 않아도 됨을 발견
되추적의 비효율 해결책 : 각 노드를 방문할 때마다 한계치(bound)를 계산
한계치(Bound) : 해당 노드로부터 가지를 뻗어나가서(branch) 얻을 수 있는 해답치의 한계 값
0/1 Knapsack Problem의 최고 우선 검색을 사용한 한정분기(Branch and Bound) 전략

1. 그 노드의 profit과 weight를 계산한다.
2. 그 노드의 bound를 계산한다.
3. 현재 노드의 profit이 maxprofit보다 크면 maxprofit 값을 경신한다.
4. (weight < M) && (bound > maxprofit)이면, 유망하다고 보고 가지를 뻗어(Branch) 나간다.
최고 우선 검색 (Best-First Search) : 최적의 해답에 더 빨리 도달하기 위한 전략
1. 주어진 노드의 모든 자식 노드를 검색한 후,
2. 유망한 노드인지를 살펴보고,
3. 그 중에서 가장 좋은(최고의) 한계치(bound)를 가진 노드를 우선적 으로 확장하여 평가 후 큐에 삽입
3-1. 최고의 한계를 가진 노드를 우선적으로 선택하기 위해서 우선순위 큐(Priority Queue) 사용
3-2. Top Priority: bound 값이 가장 큰 노드
본론
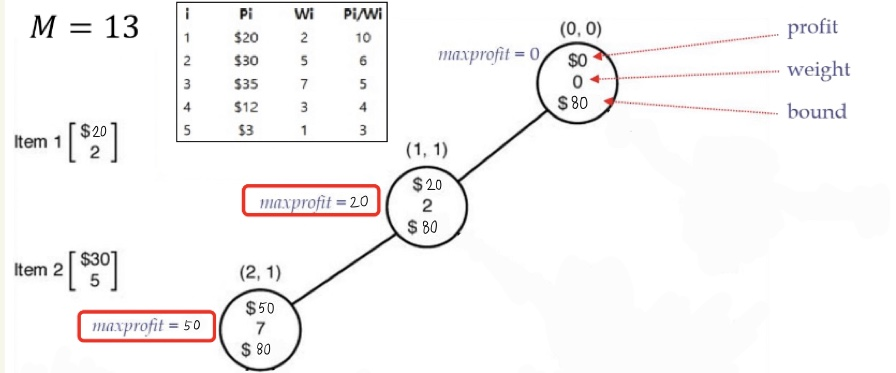
0-1 Knapsack Problem에서 배낭의 한계 무게가 13 (즉 𝑀 = 13)이고, 보석 아이템이 아래 표와 같이 주어질 때, 최고 우선 검색을 사용한 한정 분기(Branch and Bound)에 대한 상태 공간 트리를 제시하고, 상태 공간 트리 내에서 방문한 전체 노드 수를 비교하시오.
(0,0)
1) (0,0)에서 profit = 0, weight = 0 이므로, maxprofit = 0입니다.
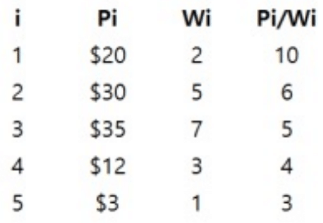
2) (0,0) 에서 bound 값을 구해보겠습니다.
2 + 5 + 7 = 14 이고, 14 > 13(W의 값)이므로, 3번째 아이템을 취하면 무게의 합이 W를 넘습니다. 따라서 k = 3 이고, totweight 와 bound 는 다음과 같이 계산합니다.

3) (weight < M) && (bound > maxprofit) 이면, 유망하다고 보고 가지를 뻗어나갑니다.
( 0 < 13 ) && ( 80 > 0 ) 즉 조건을 만족하므로, (1, 1)로 방문합니다.

(1,1)
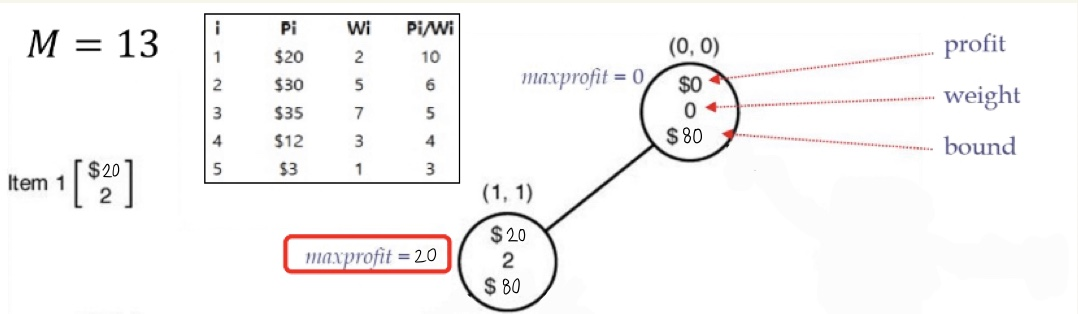
1. (1,1)에서 profit = 20, weight = 2 이므로, maxprofit = 20 입니다.
2. (1,1)에서 bound 값을 구해보겠습니다.
2 + 5 + 7 = 14 이고, 14 > 13(W의 값)이므로, 3번째 아이템을 취하면 무게의 합이 W를 넘습니다. 따라서 k = 3 이고,
totweight 와 bound 는 다음과 같이 계산합니다.
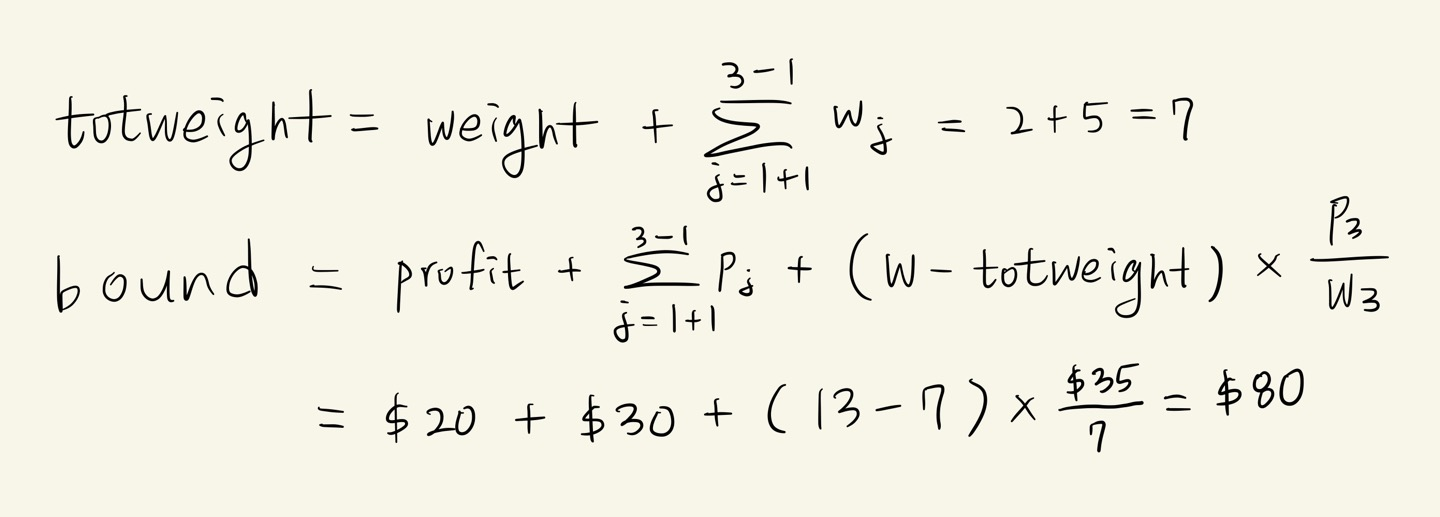
3. (weight < M) && (bound > maxprofit) 이면, 유망하다고 보고 가지를 뻗어나갑니다.
( 2 < 13 ) && ( 80 > 20 ) 즉 조건을 만족하므로, (2,1)로 방문합니다.
(2,1)
1. (2,1)에서 profit = 50, weight = 7 이므로, maxprofit = 50 입니다.
2. (2,1) 에서 bound 값을 구해보겠습니다.
2 + 5 + 7 = 14 이고, 14 > 13(W의 값)이므로, 3번째 아이템을 취하면 무게의 합이 W를 넘습니다. 따라서 k = 3 이고,
totweight 와 bound 는 다음과 같이 계산합니다.
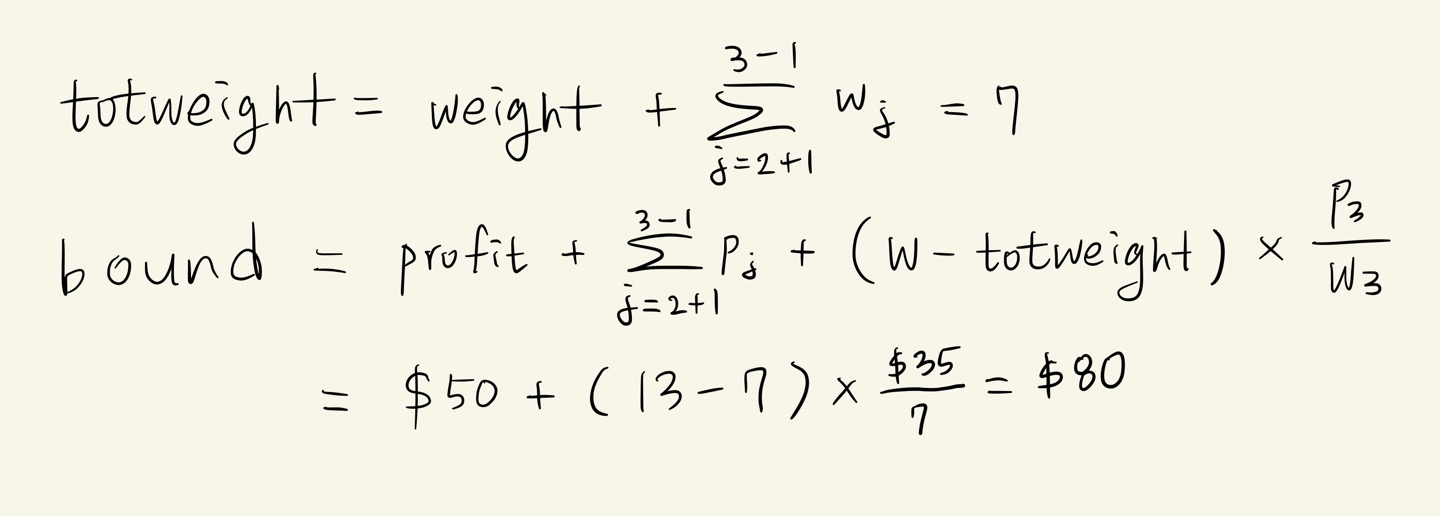
3. (weight < M) && (bound > maxprofit) 이면, 유망하다고 보고 가지를 뻗어나갑니다.
( 7 < 13 ) && ( 80 > 50 ) 즉 조건을 만족하므로, 가지를 뻗어나갑니다.
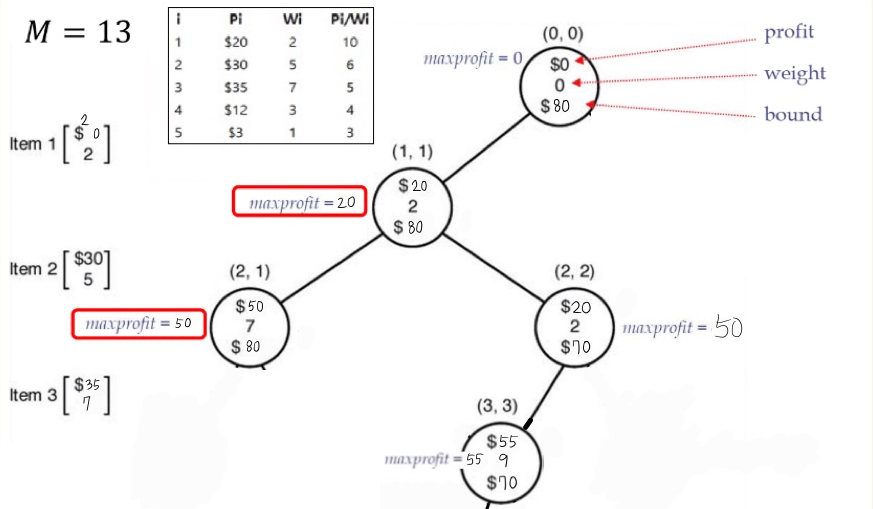
(2,2)
1. (2,2)에서 profit = 20, weight = 2 이고, maxprofit 은 (2,1)에서 구한 50입니다.
2. (2,2) 에서 bound 는 다음과 같습니다.
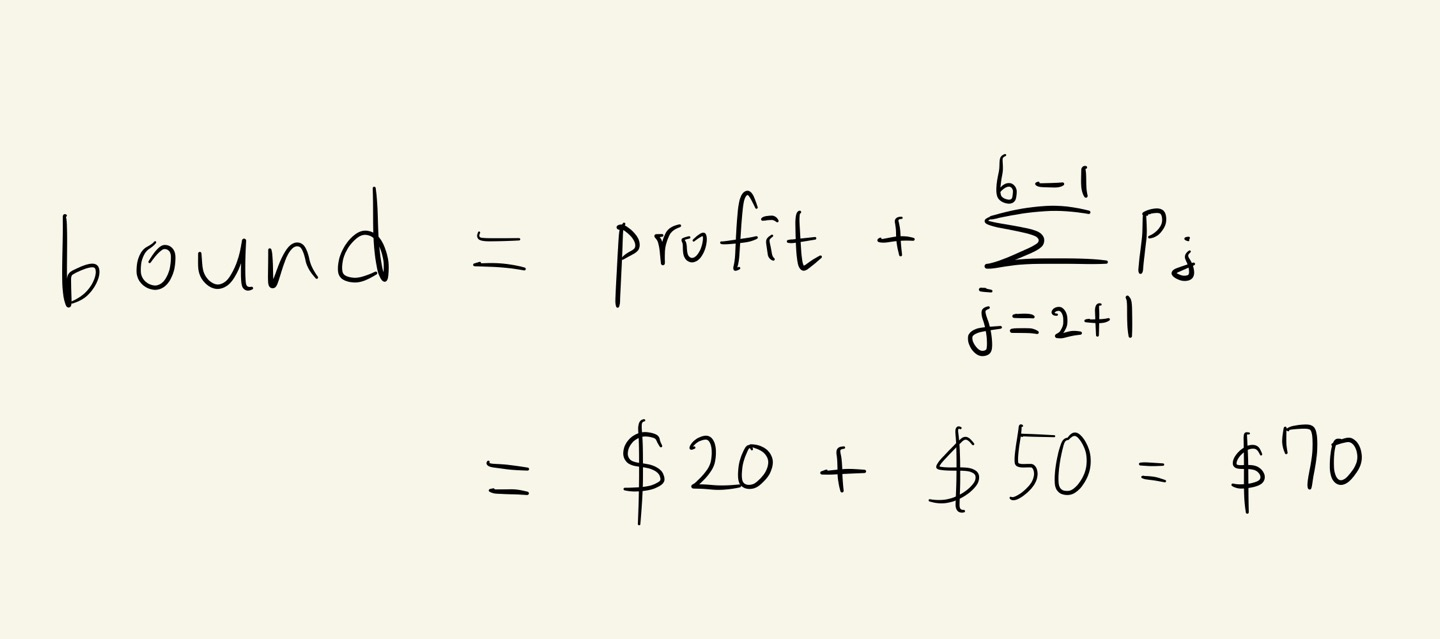
3. (weight < M) && (bound > maxprofit) 이면, 유망하다고 보고 가지를 뻗어나갑니다.
( 2 < 13 ) && ( 70 > 65 ) 조건을 만족하므로, 가지를 뻗어나갑니다.

(3,3)
1. (3,3)에서 profit = 55, weight = 9 이고, maxprofit 은 55입니다.
2. (3,3) 에서 bound 는 다음과 같습니다.
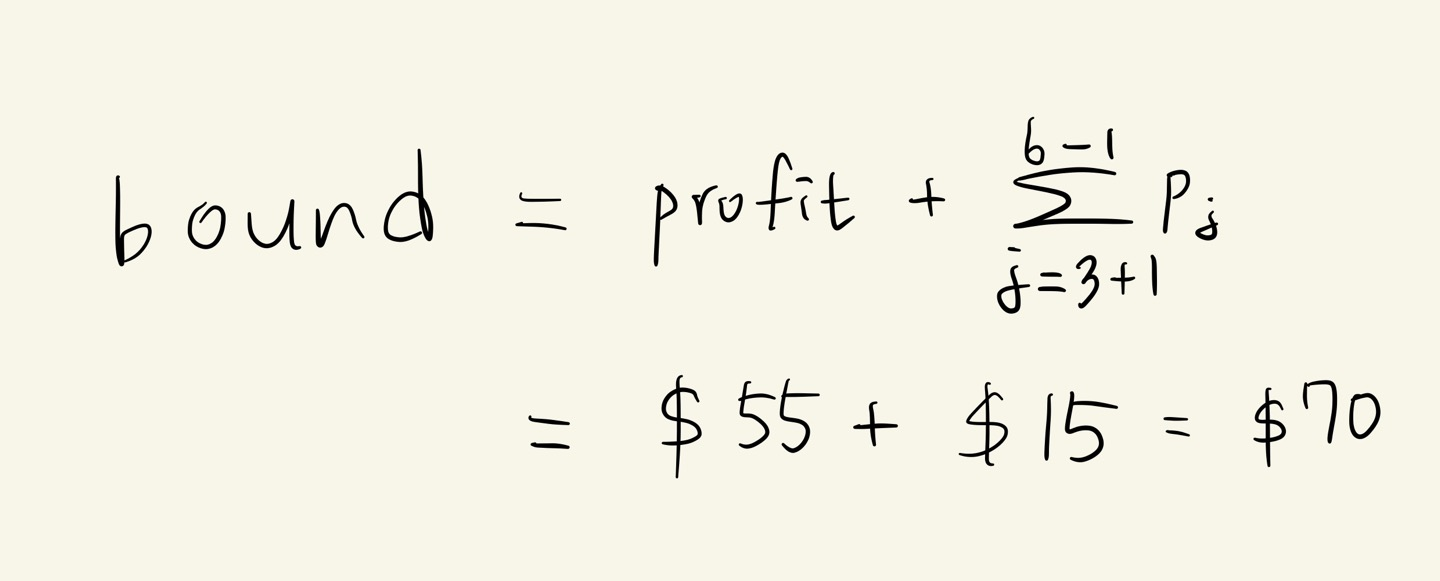
3. (weight < M) && (bound > maxprofit) 이면, 유망하다고 보고 가지를 뻗어나갑니다.
( 9 < 13 ) && ( 70 > 65 ) 조건을 만족하므로, 가지를 뻗어나갑니다.
(4,3)
1. (4,3)에서 profit = 67, weight = 12 이고, maxprofit 은 67입니다.
2. (4,3) 에서 bound 는 다음과 같습니다.
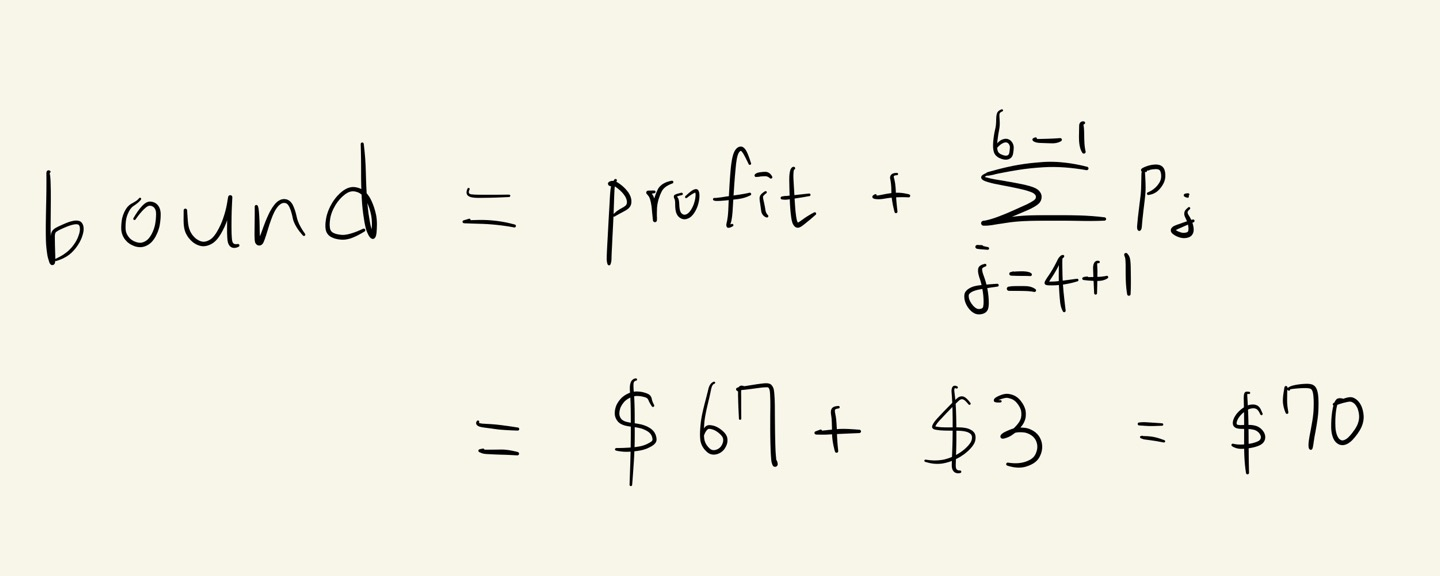
3. (weight < M) && (bound > maxprofit) 이면, 유망하다고 보고 가지를 뻗어나갑니다.
( 12 < 13 ) && ( 70 > 67 ) 조건을 만족하므로, 가지를 뻗어나갑니다.
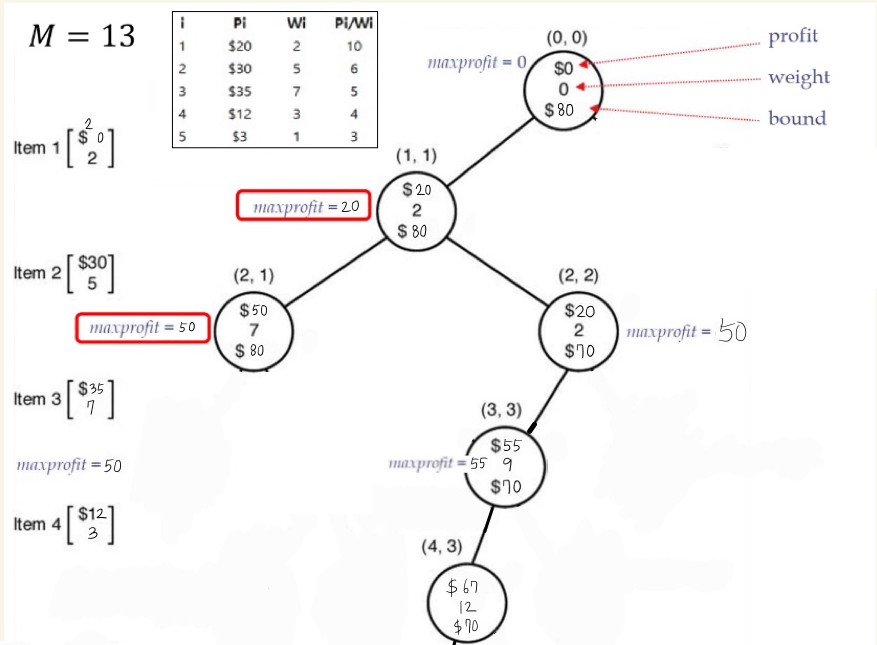
(5,3)
1. (5,3)에서 profit = 70, weight = 13 이고, maxprofit 은 70입니다.
2. (5,3) 에서 bound 는 다음과 같습니다.
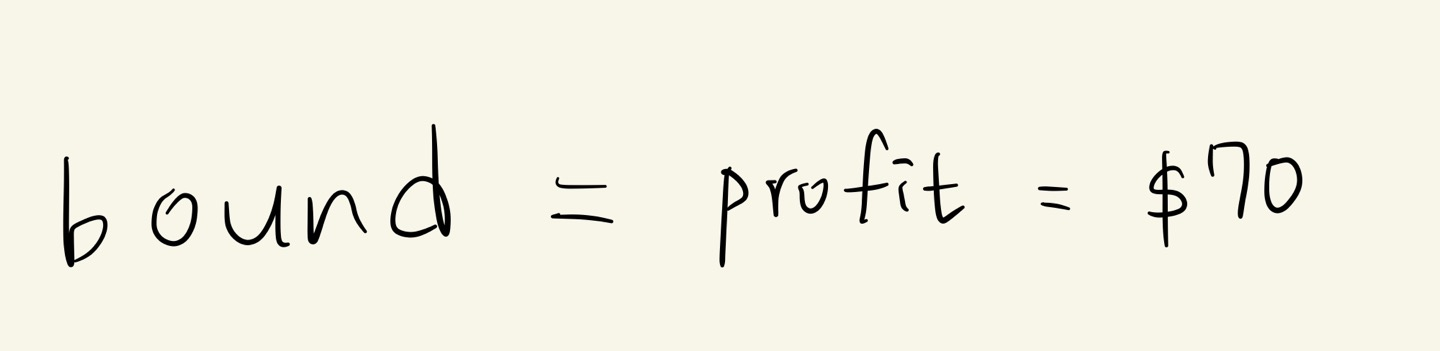
3. (weight < M) && (bound > maxprofit) 이면, 유망하다고 보고 가지를 뻗어나갑니다.
( 13 = 13 ) && ( 70 = 70 ) 조건을 만족하지 않으므로, 다음 가지로 뻗어나가지 않습니다.
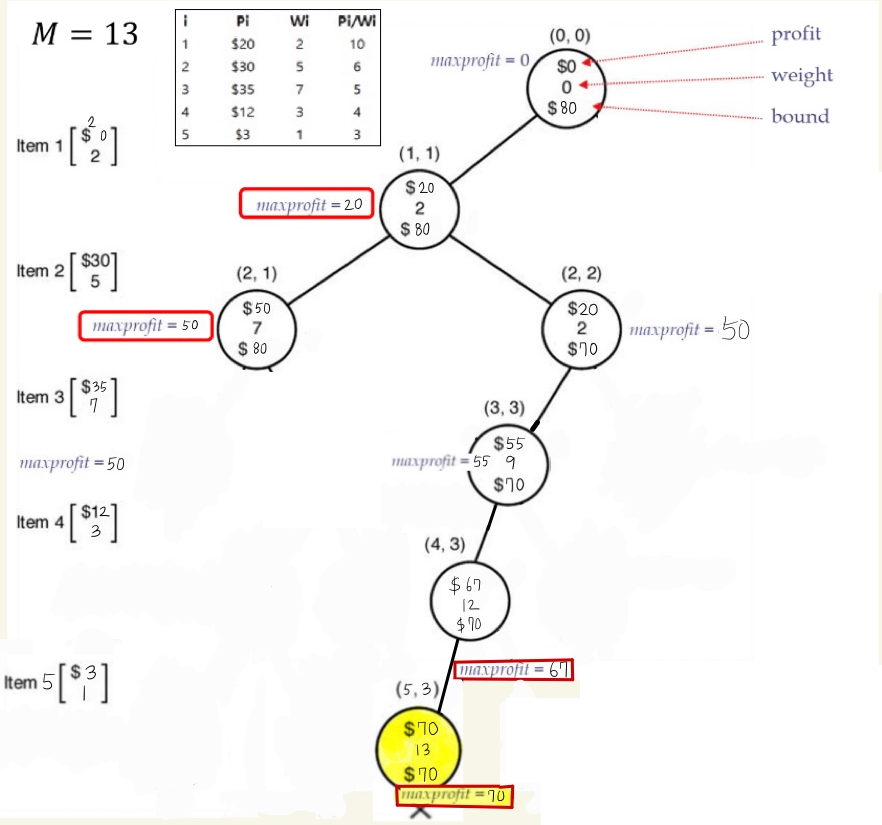
(3,2)
이제 readyQueue 에는 (3,2)와 (1,2)가 남아있습니다. 그 중 bound가 큰 (3,2)로 먼저 이동합니다.
1. (3,2)에서 profit = 50, weight = 7 이므로, maxprofit = 50 입니다.
2. (3,2) 에서 bound 값을 구해보겠습니다.
2 + 5 + 3 + 1 = 11 입니다. 즉, 3번째 아이템을 제외하고 모든 아이템을 더해도 합이 W를 초과하지 않습니다.
따라서 k=6이고, bound 는 다음과 같이 계산합니다.
이미 끝까지(k=6) 도달하였기 때문에, 가정을 통해 totweight을 구할 필요가 없습니다.
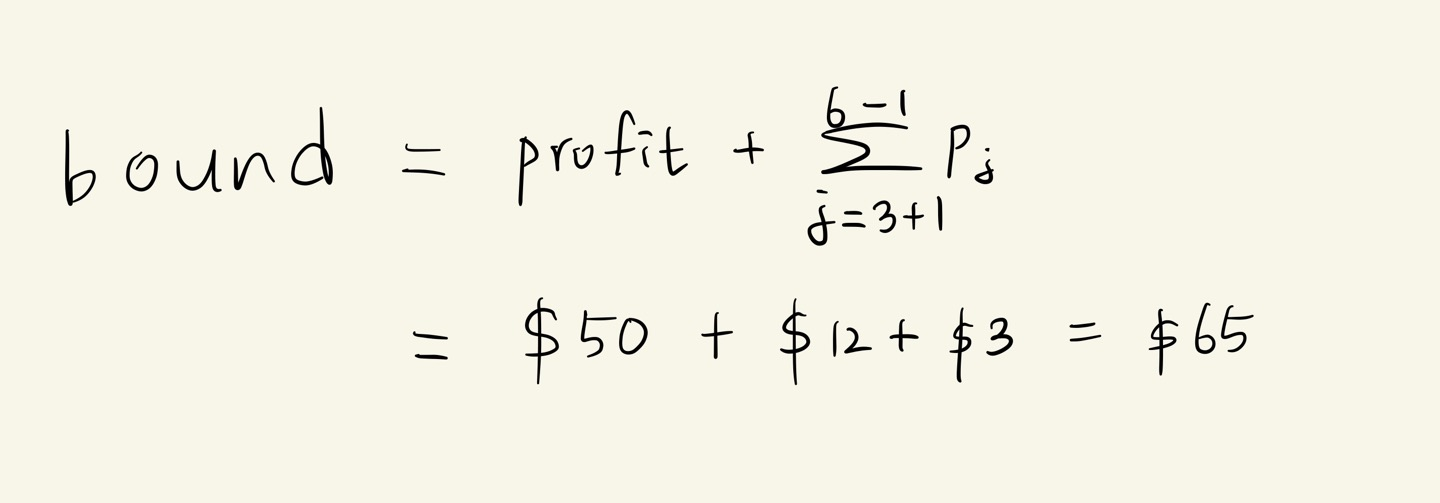
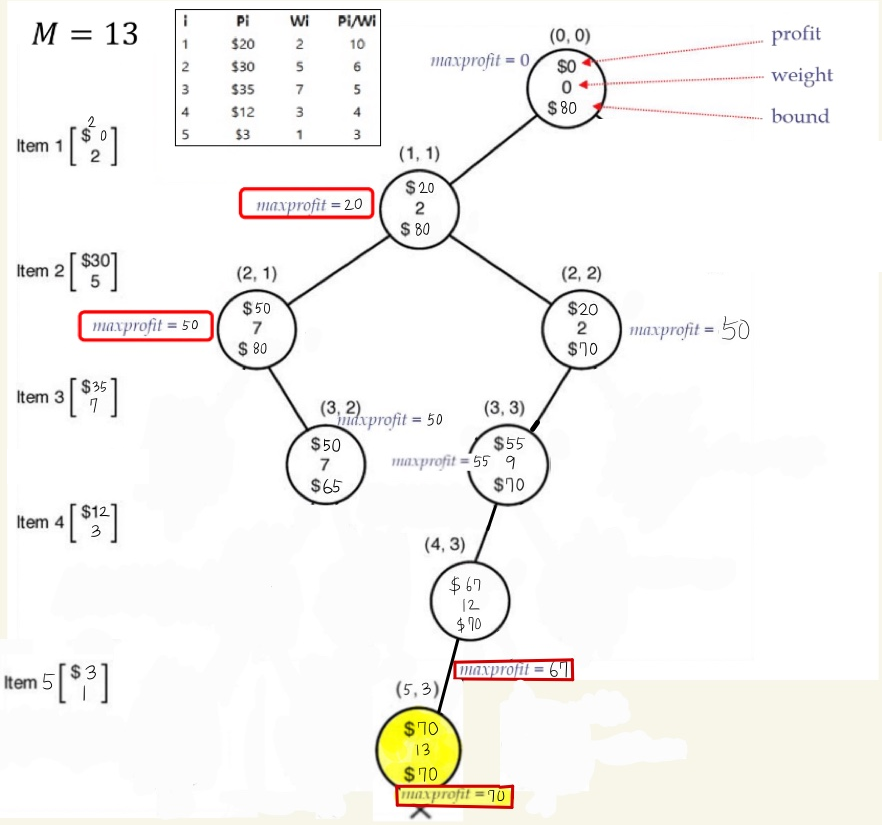
이제 readyQueue 에는 (1,2)만 남아있습니다. (1,2)로 이동합니다.
(1,2)
1. (1,2)에서 profit = 20, weight = 2 이고, maxprofit 은 (1,1)에서 구한 20입니다.
2. (1,2) 에서 bound 는 다음과 같습니다.
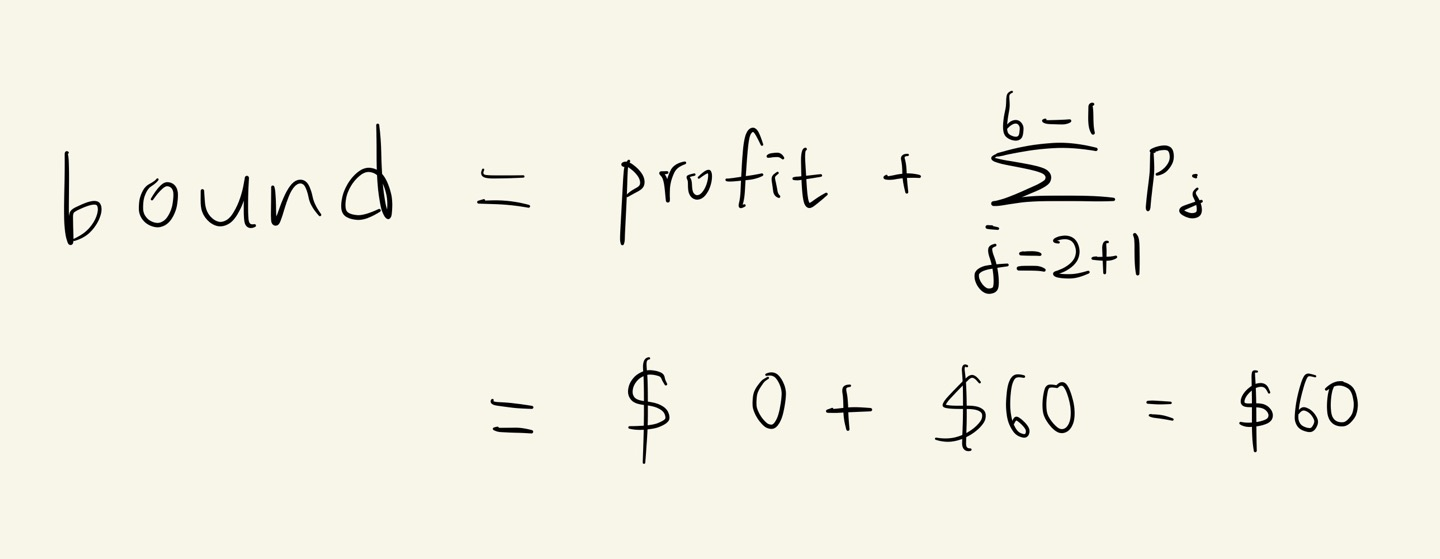
readyQueue 에서 모든 방문할 노드가 빠져나갔습니다. 종료.
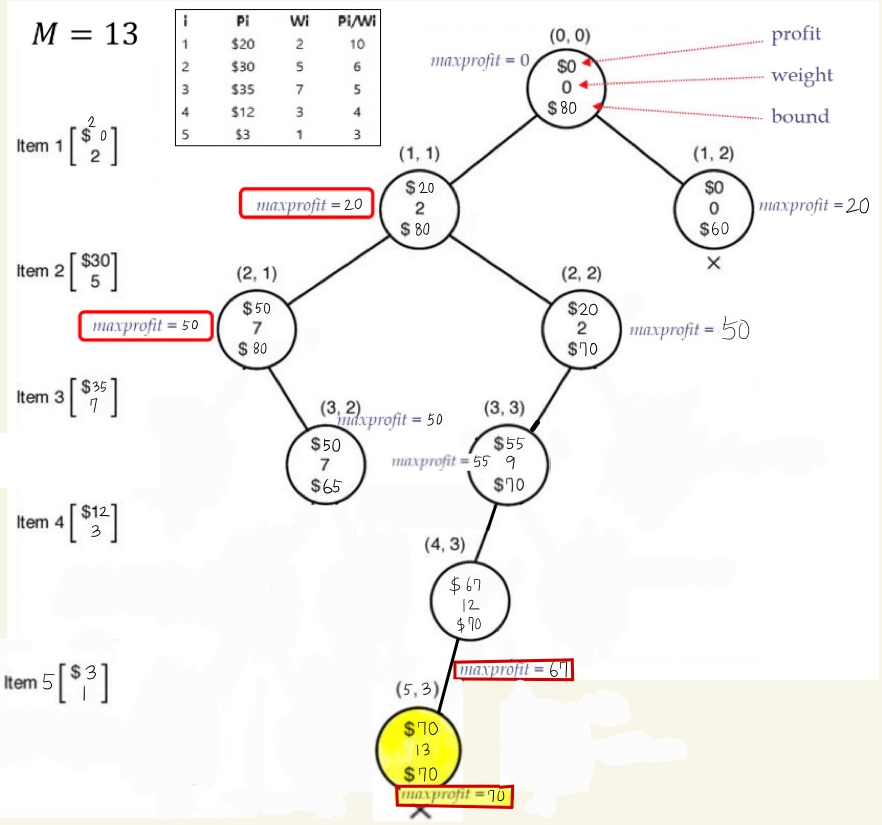
결론
최고 우선 검색을 사용한 한정 분기(Branch and Bound) 전략을 통해
최종적으로 완성된 상태 공간 트리는 다음과 같습니다.

최고 우선 탐색을 사용하여 한정 분기 전략을 사용하였을 때, 전체 방문 노드 수는 9개 입니다.
위 방법을 통해 구한 0-1 Knapsack Problem의 최적해는 아이템 1, 3, 4, 5를 가방에 넣는 것이고, 그 때의 가방의 weight는 13이고 profit은 70입니다.
최고 우선 검색을 사용한 한정 분기(Branch and Bound) 전략을 통해 상태 공간 트리의 탐색을 이해하고, 한정 분기의 작동 원리를 깨닫는 시간을 가졌습니다.
조교님 ,
강의교안에서 knapsack problem 최고 우선 검색으로 풀어내는 과정 중
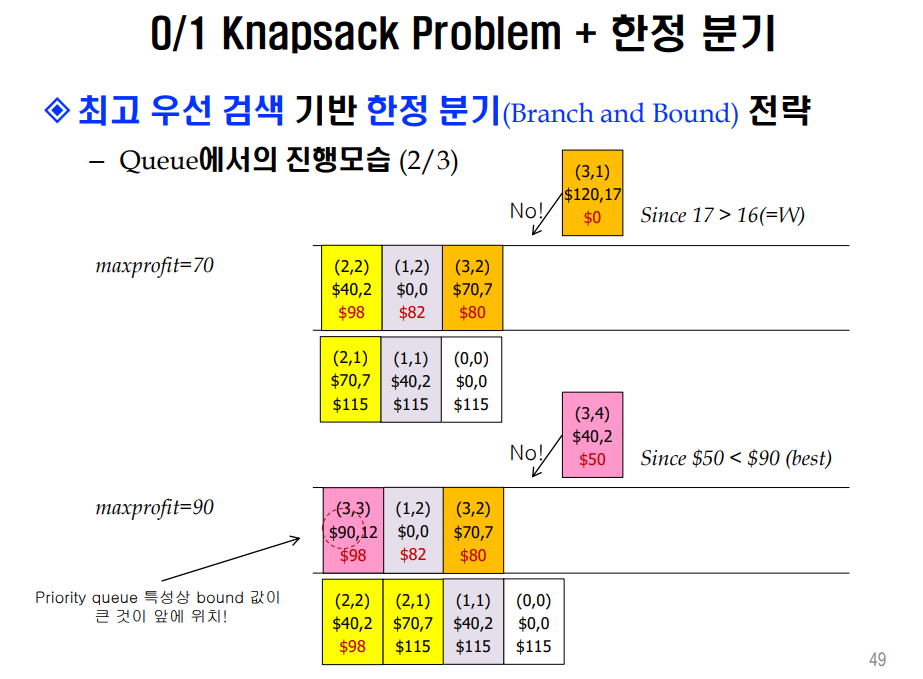
이 사진을 기준으로 보았을 때,
(3,1)은 무게가 오버돼서 priorityqueue에 못들어가고,
(3,4)는 (3,3)에서 maxprofit이 90으로 갱신되었기 때문에 못들어간다고 나와있어서,

결국 결론에는 위 사진만 탐색하는데,
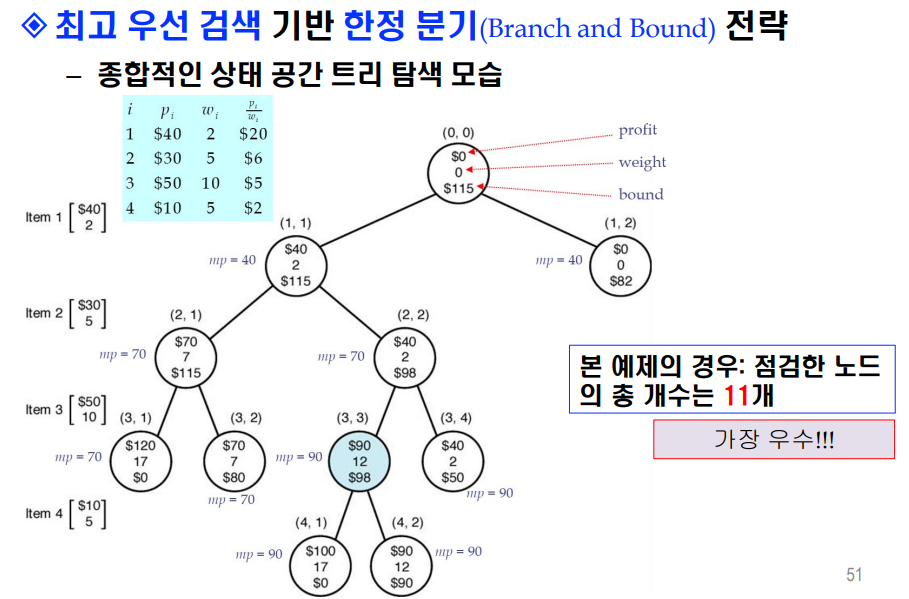
또 최종 상태 공간 트리에서는 우선순위 큐에 들어가지 않은 노드들도 트리에 포함되어 어떤 교안이 맞는지 모르겠어서
우선순위 큐 과정을 기준으로 과제를 진행하였는데, 문제되는게 있을까요?
한학기동안 감사합니다.
'파이썬' 카테고리의 다른 글
| Traveling Salesman Problem(TSP) - 최고 우선 검색 기반 한정 분기(Branch and Bound) (2) | 2022.06.15 |
|---|---|
| 0-1 Knapsack Problem - 너비 우선 검색을 사용한 한정분기 (Branch and Bound) (0) | 2022.06.15 |
| 0-1 Knapsack Problem - 깊이 우선 검색을 사용한 한정분기 (Branch and Bound) (4) | 2022.06.15 |
| 색칠 문제 - 백트래킹(Backtracking) 상태 공간 트리와 알고리즘 (0) | 2022.06.11 |
| [파이썬/Python] 허프만 알고리즘을 통한 최적 이진 문자 코드 구축 과정 분석하기 ( 허프만 코드 ) (0) | 2022.06.03 |




