| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- programmers
- php 프로그래밍 입문
- 스프링
- php 프로그래밍
- 배열
- php 프로그래밍 입문 3판
- 자바 스프링
- Flutter
- 페이코 친구코드
- 페이코 추천인코드
- 한정 분기
- php 프로그래밍 입문 예제
- SWEA
- php 프로그래밍 입문 문제풀이
- php
- php 프로그래밍 입문 연습문제
- 파이썬
- php 프로그래밍 입문 솔루션
- 최단 경로
- 자바
- Java
- C
- JAVA SPRING
- 페이코 추천인
- 플러터 개발환경 설정
- 백준
- 페이코 초대코드
- 플러터
- C언어
- spring
- Today
- Total
ImJay
[파이썬/Python] 백준 11050번 이항 계수 1 본문
[파이썬/Python] 백준 11050번 이항 계수 1
11050번: 이항 계수 1
첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 10, 0 ≤ \(K\) ≤ \(N\))
www.acmicpc.net
문제
자연수 과 정수 가 주어졌을 때 이항 계수 를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 과 가 주어진다. (1 ≤ ≤ 10, 0 ≤ ≤ )
출력
를 출력한다.
예제 입력
5 2
예제 출력
10풀이 1
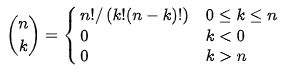
math.factorial 사용
import sys
import math
input = sys.stdin.readline
# 입력
n, k = map(int, input().split())
# 이항계수 공식
print(math.factorial(n) // (math.factorial(k) * math.factorial(n-k)))이 코드의 시간 복잡도는 `O(n)` 이다.
주어진 입력값 `n`에 대해서, `math.factorial()` 함수를 호출하여 `n!` 값을 계산하고, `k`와 `n-k`에 대한 팩토리얼 값을 각각 계산한 뒤 이를 곱하고 나누어 이항계수를 계산한다.
이항계수의 분자와 분모를 계산하는 과정에서 각각 `k`와 `n-k`번의 반복이 필요하다. `math.factorial()` 함수는 내부적으로 이 반복을 수행하기 때문에, 이 코드의 시간 복잡도는 `O(n)` 이다.
풀이 2
단순 반복문
n, k = map(int, input().split())
a = 1
b = 1
# n!/(n-k)!
for i in range(n, n-k, -1):
a *= i # n, n-1, ..., n-k+1까지 곱셈
# k!
for j in range(1, k+1):
b *= j # 1부터 k까지 곱셈
# n!/((n-k)!*k!) 계산
print(a // b) # 나눗셈 연산
주어진 입력값 `n`과 `k`에 대해서, 두 개의 변수 `a`와 `b`를 초기값 1로 설정한 뒤, `a`와 `b`를 각각 `n`부터 `n-k+1`까지의 값과 1부터 `k`까지의 값으로 업데이트하여 이항계수를 계산한다.
`for` 루프의 첫 번째 반복에서는 `a`를 `n`에서 `n-1`까지 1씩 감소하면서 `k`개의 인자에 대한 곱셈을 계산한다. 따라서 이 과정은 `O(k)`의 시간 복잡도를 가지게 된다.
두 번째 `for` 루프에서는 `b`를 1에서 `k`까지 1씩 증가하면서 `k`개의 인자에 대한 곱셈을 계산한다. 이 과정 역시 `O(k)`의 시간 복잡도를 가진다.
마지막으로 `a`와 `b`의 값을 나누어 이항계수를 계산한다. 이 연산은 상수 시간에 이루어진다.
따라서 이 코드의 시간 복잡도는 `O(k)` 이다.
참고자료
이항 계수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 조합론에서 이항 계수(二項係數, 영어: binomial coefficient)는 이항식을 이항 정리로 전개했을 때 각 항의 계수이며, 주어진 크기의 (순서 없는) 조합의 가짓수이다.
ko.wikipedia.org
[Python] 다양한 방법으로 팩토리얼(Factorial) 구해보기
Python을 통해 가능한 많은 방법으로 팩토리얼을 구해봅시다.
shoark7.github.io
로그인
www.acmicpc.net

'Solved.ac - Python > CLASS 2' 카테고리의 다른 글
| [파이썬/Python] 백준 11866번 요세푸스 문제 0 (0) | 2023.05.14 |
|---|---|
| [파이썬/Python] 백준 11650번 좌표 정렬하기 (0) | 2023.05.13 |
| [파이썬/Python] 백준 10866번 덱 (1) | 2023.05.11 |
| [파이썬/Python] 백준 10845번 큐 (0) | 2023.05.11 |
| [파이썬/Python] 백준 10828번 스택 (0) | 2023.05.10 |




