| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- php 프로그래밍 입문 예제
- spring
- 백준
- php 프로그래밍 입문 문제풀이
- 페이코 추천인코드
- php 프로그래밍 입문 3판
- php 프로그래밍 입문
- 파이썬
- php 프로그래밍 입문 연습문제
- 자바 스프링
- 페이코 추천인
- 플러터
- 배열
- 자바
- php 프로그래밍
- 스프링
- 페이코 친구코드
- SWEA
- Flutter
- 한정 분기
- C
- php
- JAVA SPRING
- 페이코 초대코드
- 최단 경로
- php 프로그래밍 입문 솔루션
- C언어
- Java
- programmers
- 플러터 개발환경 설정
- Today
- Total
ImJay
[파이썬/Python] 허프만 알고리즘을 통한 최적 이진 문자 코드 구축 과정 분석하기 ( 허프만 코드 ) 본문
허프만 알고리즘을 통한 최적 이진 문자 코드 구축 과정 분석하기 (허프만 코드)
서론
허프만 코드(Huffman Code)란 문자들로 이루어진 데이터 파일 크기를 작게 만들기 위해 문자 각각을 코드화 하는 방법 중 하나입니다. 더 자주 출현하는 문자에 대하여 더 짧은 코드를 할당합니다.
최적 이진 코딩 문제(Optimal Binary Code)는 주어진 텍스트 파일에 있는 문자들을 이진 코드로 표현하기 위해 필요한 비트의 개수가 최소가 되는 이진 문자 코드를 찾는 문제입니다.
즉, 허프만 코딩 문제는 주어진 문자 집합에 대해 최적 코드에 해당하는 이진 트리를 구축하여 최적 이진 문자 코드(Huffman code)를 만들어 보는 문제입니다.
본론
허프만 코딩 문제 알고리즘
1) Priority Queue 에서 차례로 두 개를 선택하여
2) 선택된 각각을 left와 right child에 배치하는 새로운 노드를 생성하여 binary subtree 생성
3) 새로운 노드의 빈도수로서 선택된 두 빈도수의 합을 지정
4) 그 새로운 노드를 Priority Queue에 삽입
Priority Queue 의 우선순위
1) 더 낮은 빈도 수의 노드
2) 새롭게 구성된 노드
3) 더 낮은 알파벳의 노드
문제 1. 허프만의 알고리즘을 사용하여 다음 표에 있는 글자들에 대한 최적 이진 트리를 구축하는 과정을 제시하시오.

N=1
1) Priority Queue 에서 차례로 두 개를 선택하여

2) 선택된 각각을 left와 right child에 배치하는 새로운 노드를 생성하여 binary subtree 생성
3) 새로운 노드의 빈도수로서 선택된 두 빈도수의 합을 지정

4) 그 새로운 노드를 Priority Queue에 삽입
- Priority Queue 의 우선순위에서, 1순위인 더 낮은 빈도 수가 둘 다 같으므로, 2순위인 새롭게 구성된 노드로 구분

N=2
1) Priority Queue 에서 차례로 두 개를 선택하여

2) 선택된 각각을 left와 right child에 배치하는 새로운 노드를 생성하여 binary subtree 생성
3) 새로운 노드의 빈도수로서 선택된 두 빈도수의 합을 지정
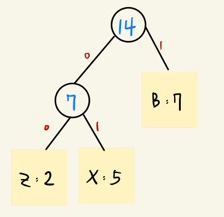
4) 그 새로운 노드를 Priority Queue에 삽입

N=3
1) Priority Queue 에서 차례로 두 개를 선택하여

2) 선택된 각각을 left와 right child에 배치하는 새로운 노드를 생성하여 binary subtree 생성
3) 새로운 노드의 빈도수로서 선택된 두 빈도수의 합을 지정

4) 그 새로운 노드를 Priority Queue에 삽입

N=4
1) Priority Queue 에서 차례로 두 개를 선택하여

2) 선택된 각각을 left와 right child에 배치하는 새로운 노드를 생성하여 binary subtree 생성
3) 새로운 노드의 빈도수로서 선택된 두 빈도수의 합을 지정

4) 그 새로운 노드를 Priority Queue에 삽입

N=5
1) Priority Queue 에서 차례로 두 개를 선택하여

2) 선택된 각각을 left와 right child에 배치하는 새로운 노드를 생성하여 binary subtree 생성
3) 새로운 노드의 빈도수로서 선택된 두 빈도수의 합을 지정

4) 그 새로운 노드를 Priority Queue에 삽입

N=6
1) Priority Queue 에서 차례로 두 개를 선택하여

2) 선택된 각각을 left와 right child에 배치하는 새로운 노드를 생성하여 binary subtree 생성
3) 새로운 노드의 빈도수로서 선택된 두 빈도수의 합을 지정

4) 그 새로운 노드를 Priority Queue에 삽입

선택할 노드가 한 개 밖에 없으므로, 완성.
문제 2. 위에서 제시한 최적 이진 트리를 기반으로 각 주어진 문자에 대한 최적 전치 코드 허프만 코드를 제시하시오.

허프만의 알고리즘을 사용하여 완성된 최적 이진트리로 만든 허프만 코드는 다음과 같습니다.

기존 아스키 코드와 비교했을 때 최적 이진 트리를 기반으로 만든 허프만 코드의 효율성은 다음과 같습니다.
| 문 자 | 빈 도 | 원래(ASCII) 크기 | 압축된 크기 | 차이 |
| A | 12 | 7 * 12 = 84 | 2 * 12 = 24 | 60 |
| B | 7 | 7 * 7 = 49 | 3 * 7 = 21 | 28 |
| I | 18 | 7 * 18 = 126 | 2 * 18 = 36 | 90 |
| M | 10 | 7 * 10 = 70 | 3 * 10 = 30 | 40 |
| S | 9 | 7 * 9 = 63 | 3 * 9 = 27 | 36 |
| X | 5 | 7 * 5 = 35 | 4 * 5 =20 | 15 |
| Z | 2 | 7 * 2 = 14 | 4 * 2 = 8 | 6 |
| 계 | 63 | 441 | 166 | 275 |
결론
최적 이진 트리가 실생활에 쓰이는 방법에 대해 허프만 알고리즘과 허프만 코드를 통해 배울 수 있었습니다.
사용 빈도 수에 따라 비트 수를 달리하여 크기를 줄이는 방법은 효율적으로 보였으며,
그 빈도 수에 따라 코드 길이를 정하는 방법을 정하는 알고리즘을 이진 트리를 통해 만들어 낸 것 또한 이진 트리의 쓰임에 대해 알면서 응용하는 방법 중 하나를 배운 것 같아 뜻 깊은 시간이었습니다.
'파이썬' 카테고리의 다른 글
| 0-1 Knapsack Problem - 깊이 우선 검색을 사용한 한정분기 (Branch and Bound) (4) | 2022.06.15 |
|---|---|
| 색칠 문제 - 백트래킹(Backtracking) 상태 공간 트리와 알고리즘 (0) | 2022.06.11 |
| [파이썬/Python] 최단 경로 알고리즘 작동원리 이해하기 ( Floyd-washall ) (0) | 2022.06.03 |
| [파이썬/Python] 최단 경로 알고리즘 작동원리 이해하기 ( Dijkstra ) (0) | 2022.06.02 |
| [파이썬/Python] 최소 비용 신장 트리 알고리즘 작동원리 이해하기 ( Prim / Kruskal ) (0) | 2022.06.02 |




