| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 파이썬
- spring
- 백준
- php 프로그래밍 입문 문제풀이
- 페이코 추천인
- php 프로그래밍 입문 3판
- 자바
- 스프링
- php 프로그래밍
- 플러터 개발환경 설정
- 최단 경로
- Flutter
- 자바 스프링
- C언어
- php
- 페이코 친구코드
- SWEA
- Java
- JAVA SPRING
- 한정 분기
- php 프로그래밍 입문 예제
- 플러터
- programmers
- php 프로그래밍 입문
- 페이코 초대코드
- 배열
- php 프로그래밍 입문 연습문제
- C
- php 프로그래밍 입문 솔루션
- 페이코 추천인코드
- Today
- Total
ImJay
[파이썬/Python] 최단 경로 알고리즘 작동원리 이해하기 ( Dijkstra ) 본문
[파이썬/Python] 최단 경로 알고리즘 작동원리 이해하기 ( Dijkstra )
서론
[파이썬/Python] 최단 경로 알고리즘 구현하기 ( Dijkstra / Bellman-ford / floyd-warshall )
최단 경로 알고리즘 구현하기 ( Dijkstra / Bellman-ford / floyd-warshall ) 서론 최단 경로(Shortest Paths)는 두 정점 사이의 경로를 구성하는 모든 간선의 가중치 합이 최소인 경로를 말합니다. 최단 경..
develop247.tistory.com
이전 시간 구현하였던 Dijkstra 알고리즘의 작동원리에 대해 간단한 예제를 통해 그림으로 이해해보려고 합니다.
본론
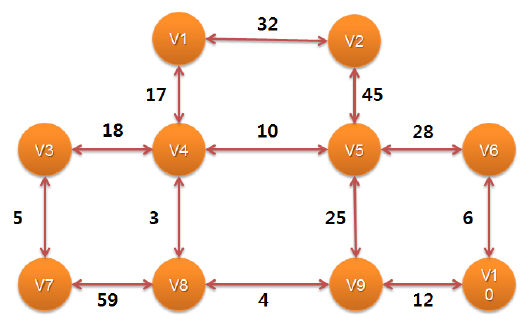
문제 1. Dijkstra 알고리즘을 이용하여 위 그래프의 v4를 시작으로 하는 최소비용 신장 트리를 구하는 과정을 제시하시오.
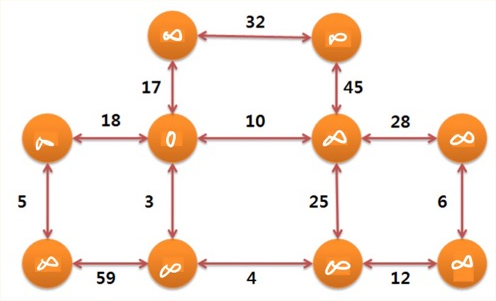
처음 start_node = 4이므로, d[4] = 0 이 저장됩니다.
나머지 노드들은 무한으로 초기화했기 때문에 무한대가 담겨 있습니다.
def extract_min(self, V_minus_S, d):
min = sys.maxsize
selected_node = None
for node in V_minus_S: # 트리 외부 노드들을 비교
if d[node] < min: # d 값이 가장 작다면
min = d[node] # d 값으로 저장
selected_node = node # 최소 가중치 간선 노드
return selected_node이전에 작성했던 코드 중 인접 노드에서 최단 경로 노드를 반환해주는 함수입니다.

extract_min 함수를 통해 반환된 최소 가중치 노드는 4이고, d[4] = 0 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
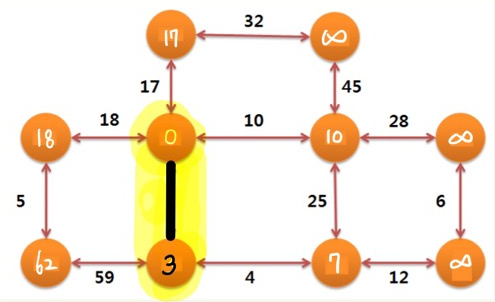
extract_min 함수를 통해 반환된 최소 가중치 노드는 8이고, d[8] = d[4] + 3 = 3 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
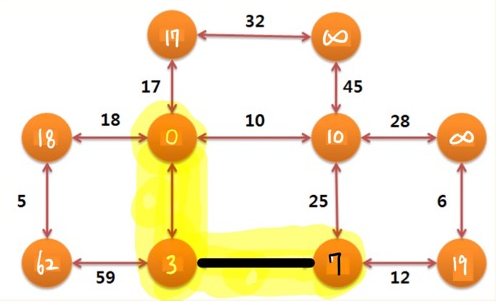
extract_min 함수를 통해 반환된 최소 가중치 노드는 9이고, d[9] = d[8] + 4 = 7 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
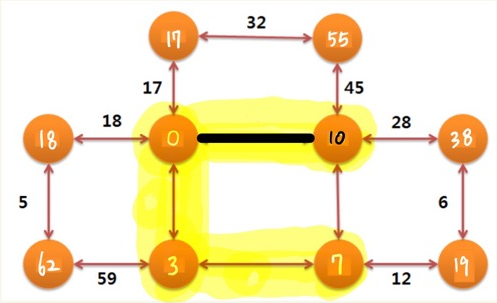
extract_min 함수를 통해 반환된 최소 가중치 노드는 5이고, d[5] = d[4] + 10 = 10 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
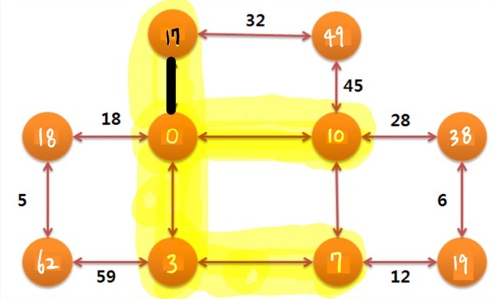
extract_min 함수를 통해 반환된 최소 가중치 노드는 1이고, d[1] = d[4] + 17 = 17 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
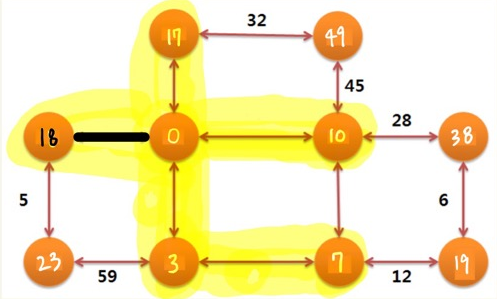
extract_min 함수를 통해 반환된 최소 가중치 노드는 3이고, d[3] = d[4] + 18 = 18 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.

extract_min 함수를 통해 반환된 최소 가중치 노드는 10이고, d[10] = d[9] + 12 = 19 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
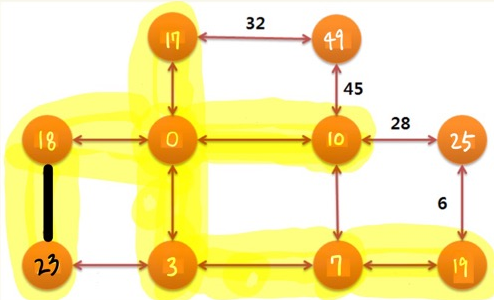
extract_min 함수를 통해 반환된 최소 가중치 노드는 7이고, d[7] = d[3] + 5 = 23 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.

extract_min 함수를 통해 반환된 최소 가중치 노드는 6이고, d[6] = d[10] + 6 = 25 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
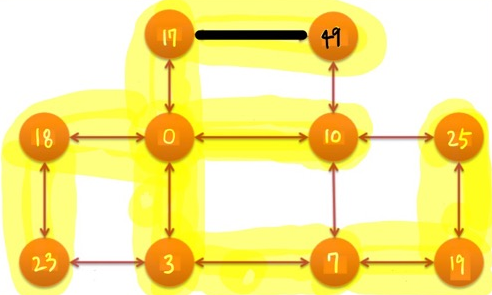
extract_min 함수를 통해 반환된 최소 가중치 노드는 2이고, d[2] = d[1] + 32 = 49 입니다.
인접 노드들까지의 최단경로가 d[인접노드] 에 저장된 것을 확인할 수 있습니다.
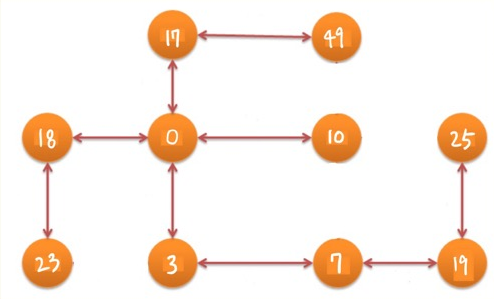
djikstra 알고리즘을 통해 완성된 최단 경로입니다.
dijkstra_adjacency_list = {
'1': {'2': 32, '4': 17},
'2': {'1': 32, '5': 45},
'3': {'4': 18, '7': 5},
'4': {'1': 17, '3': 18, '5': 10, '8': 3},
'5': {'2': 45, '4': 10, '6': 28, '9': 25},
'6': {'5': 28, '10': 6},
'7': {'3': 5, '8': 59},
'8': {'4': 3, '7': 59, '9': 4},
'9': {'5': 25, '8': 4, '10': 12},
'10': {'6': 6, '9': 12}
}그래프를 제대로 그렸는지 확인하기 위해 지난번 작성한 코드에서 딕셔너리를 수정하여 컴파일해보았습니다.

출력 결과 직접 그려본 그래프와 코드의 결과가 일치함을 확인할 수 있었습니다.
결론
지난 시간 다익스트라 알고리즘의 코드를 작성해보면서, 알고리즘의 원리에 대해 이해하였습니다.
이번 시간 그 알고리즘의 작동 원리를 그림을 통해 그려보면서 보다 자세하게 알고리즘의 작동 원리에 대해 이해하는 시간을 가질 수 있었습니다.
특히 직접 그림을 그리며 알고리즘의 작동 원리를 확인해보는게 훨씬 빠르고 쉽게 알고리즘을 이해할 수 있는 것 같습니다..
'파이썬' 카테고리의 다른 글
| [파이썬/Python] 허프만 알고리즘을 통한 최적 이진 문자 코드 구축 과정 분석하기 ( 허프만 코드 ) (0) | 2022.06.03 |
|---|---|
| [파이썬/Python] 최단 경로 알고리즘 작동원리 이해하기 ( Floyd-washall ) (0) | 2022.06.03 |
| [파이썬/Python] 최소 비용 신장 트리 알고리즘 작동원리 이해하기 ( Prim / Kruskal ) (0) | 2022.06.02 |
| [파이썬/Python] 동적 프로그래밍 - 행렬 곱셈 순서 계산하기 ( Brute-Force Algorithm ) (0) | 2022.06.02 |
| [파이썬/Python] 최단 경로 알고리즘 구현하기 ( Dijkstra / Bellman-ford / floyd-warshall ) (0) | 2022.06.01 |




